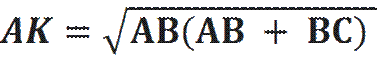-Учебные материалы Шарапова М.П.

Веб-сайт: http://sharapovmp.ru,

http://www.sharapovmp.ru

© Шарапов Михаил Петрович, 2022

E-mail: autocad1012@yahoo.com

На подступах к ОГЭ

Задача по планиметрии. Прямая и окружность

Условие

Дана окружность и точка A вне этой окружности.

Из точки A проведена касательная к этой окружности, точка касания K.

Из точки A проведена прямая, пересекающая эту окружность в точках B и C.

Известны длины отрезков AB и BC.

Найти:

Длину отрезка AK,

Решение

Прежде, чем рисовать чертеж, подумаем.

Касательная – перпендикулярна радиусу, проведенному в точку касания.

Начертим радиус из точки касания до точки, где все радиусы встречаются – до центра окружности, точки O.

Рука раззуделась!

Проведем еще пару радиусов: BO и CO,

Унимаем зуд – больше точек на окружности нет.

Теперь раззуделся глаз.

BC – хорда, «обрамленная» двумя радиусами.

Перпендикуляр к хорде, проведенный из центра окружности, делит хорду пополам.

И его нарисуем.

Вот!

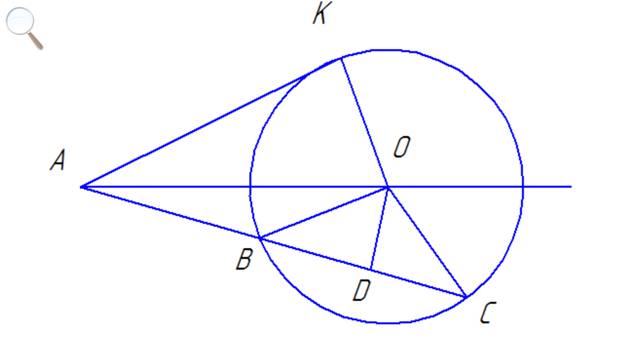
Итак

AK⊥KO

DO⊥BC

BD-DC

KO = BO = CO.

Получили два прямоугольных треугольника с общей гипотенузой: △AKO и △ADO.

Из △AKO по теореме Пифагора:

AO² = AK² + KO²

Из △ADO по теореме Пифагора:

AO² = AD² + DO²

AD² = (AB + BD)²

BD = BC/2

DO² найдем из прямоугольного треугольника △ВDO.

DO² = BO² - BD²

Подставляем

AO² = AD² + DO²

Куда подставляем	Что подставляем или как преобразуем	Что получаем
AO^2 = AD^2 + DO^2	AD^2 =(AB + BD)^2	AO^2 = (AB + BD)^2 + DO^2
AO^2 = (AB + BD)^2 + DO^2	DO^2 = BO^2 - BD^2	AO^2 = (AB + BD)^2 + BO^2 - BD^2
(AB + BD)^2	Квадрат суммы	(AB + BD)^2=AB^2 + 2×AB×BD + BD^2
AO^2 = (AB + BD)^2 + BO^2 - BD^2	(AB + BD)^2=AB^2 + 2×AB×BD + BD^2	AO^2 = AB^2 + 2×AB×BD + BD^2 + BO^2 - BD^2
AO^2 = AB^2 + 2×AB×BD + BD^2 + BO^2 - BD^2	Сокращаем BD^2	AO^2 = AB^2 + 2×AB×BD + BO^2
AO^2 = AB^2 + 2×AB×BD + BO^2	BD = BC/2	AO^2 = AB^2 + 2×AB× BC/2+ BO^2
AO^2 = AB^2 + 2×AB× BC/2+ BO^2	Сокращаем 2 и 2.	AO^2 = AB^2 + AB× BC+ BO^2
AO^2 = AB^2 + AB× BC+ BO^2	AO^2 = AK^2 + KO^2	AK^2 + KO^2 = AB^2 + AB× BC+ BO^2
AK^2 + KO^2 = AB^2 + AB× BC+ BO^2	KO = BO	AK^2 + BO^2 = AB^2 + AB× BC+ BO^2
AK^2 + BO^2 = AB^2 + AB× BC+ BO^2	Сокращаем BO^2	AK^2 = AB^2 + AB× BC
AK^2 = AB^2 + AB× BC	Вынесем общий множитель AB.	AK^2 = AB(AB + BC)
AK^2 = AB(AB + BC)	Извлекаем корень квадратный из выражения в левой части и – не менее квадратный корень из выражения в правой части.
	=AK

AK² = AB(AB + BC)