-Учебные материалы Шарапова М.П.
Веб-сайт: http://sharapovmp.ru,
© Шарапов Михаил Петрович, 2022, Решение задачи
E-mail: autocad1012@yahoo.com
На подступах к ЕГЭ
Решение задачи 2
Условие
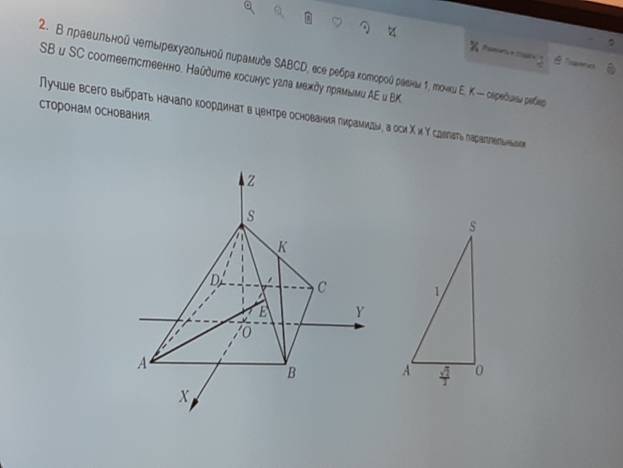
Решение
В условии задачи
содержится ключ к ее решению.
Иначе ее
нельзя было бы решить.
Косинус угла
фигурирует в теореме косинусов и в формуле скалярного произведения векторов.
Уже выбрана
система координат.
Значит,
решать надо через скалярное произведение векторов
и 
.
Скалярное
произведение векторов 
и 
выражается так:
, где
- x-координаты векторов и 
y-координаты векторов и z-координаты векторов и 
– угол между векторами и - искомая
величина.
Координаты
вектора находят как разности соответствующих координат точек конца и начала
вектора.
Координаты
точек:
A(1/2; -1/2; 0)
E(-1/4; -1/4; 
)
B(-1/2; -1/2; 0)
K(-1/4; 1/4; )
Модули
векторов вычислить легко, если вспомнить, что все ребра равны.
Значит
треугольники боковых граней равносторонние и равны между собой.
А AE и BK – медианы, а, следовательно и высоты.
Следовательно,
модули этих векторов равны 
Найдем сумму
произведений одноименных координат.
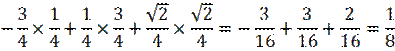
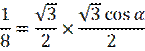
