Учебные материалы Шарапова М.П.

Сравнение иррациональных выражений разностей квадратных корней

© Шарапов Михаил Петрович, 2021

Сравнить

и

Преобразуем эти разности в дроби.

Используем формулу разности квадратов.

Умножим и разделим

На

Получим

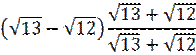
Бессмысленное какое-то действие, ведь на единицу умножили.

Да, но мы эту единицу потом «разделим на части» и каждую «часть» используем по-своему.

Действие бессмысленное, на первый взгляд, но полезное.

В числителе будет разность квадратов корней

=

Квадрат квадратного корня это то, что под корнем.

Значит, дробь станет такой

И даже такой

Вспомним, с чего мы начали

И подставим то, чем закончили

«Набросимся» на вторую разность.

Прозорливцы уже знают, чем дело окончится.

Преобразуем вторую разность в дробь.

Используем формулу разности квадратов.

Умножим и разделим

На

Получим

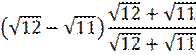
Бессмысленное какое-то действие, ведь на единицу умножили.

Да, но мы эту единицу потом «разделим на части» и каждую «часть» используем по-своему.

Действие бессмысленное, на первый взгляд, но полезное.

В числителе будет разность квадратов корней

=

Квадрат квадратного корня это то, что под корнем.

Значит, дробь станет такой

И даже такой

Вспомним, с чего мы начали

И подставим то, чем закончили

Значит,

Если надо

Сравнить

и

надо

Сравнить

и

И

Сравниваем две дроби с равными числителями.

У каждой числитель единица.

Сравниваем знаменатели

Сократим корни из 12 - равные слагаемые в левой и правой частях.

Так как 13 > 11, по свойству квадратных корней

Следовательно

А это значит

Числители дробей равны и положительны. Знаменатели положительны. Знаменатель левой дроби больше знаменателя правой дроби, значит, левая дробь меньше правой дроби.

Вспомним, какие исходные выражения равны этим дробям.

Следовательно