Учебные материалы Шарапова М.П.
Решение тригонометрического уравнения
2
+ sin x cos x + 
(sin 2x + 
) = 0
© Шарапов Михаил Петрович, 2022-05-24
Дано:
Уравнение
2 + sin x cos x + (sin 2x +
) = 0
Требуется:
1.
Решить
уравнение
2 + sin x cos x + (sin
2x +) =
0
2.
Найти
корни уравнения
2 + sin x
cos x + (sin
2x + ) =
0,
принадлежащие промежутку
[
; 
].
Решение
Исходное уравнение
2 + sin x cos x + (sin
2x + ) =
0,
Готовой формулы для решения такого уравнения нет.
Для уравнения, например, такого:
sin x = 0,
есть, а для «нашего» уравнения нет.
Именно поэтому ее и предлагается вывести, т.е. – решить исходное уравнение.
Преобразуем уравнение.
Выразим sin 2x:
sin 2x = 2sin x cos x.
Вместо sin 2x в
исходное уравнение подставим 2sin x cos x.
Получим:
2 + sin x cos x + (2sin
x cos x + ) =
0.
В выражении есть суммы произведений, имеющих общие множители.
Сгруппируем первые два слагаемых:
2 + sin x cos x
и вынесем множитель sin x за скобки.
Получим:
2 + sin x cos x = (sin x)(2 sin x + cos x).
Сгруппируем два других слагаемых.
2sin x cos x +
и вынесем множитель cos x за скобки.
Получим:
2sin x cos x + = (cos x)(2 sin x + cos x).
Исходное уравнение стало таким:
(sin x)(2 sin x + cos x) + (cos x)(2 sin x + cos x) = 0.
Заметили еще один общий множитель?
Вот он:
(2 sin x + cos x).
Вынесем его за скобки.
А, что еще делать с общим множителем!?
Исходное уравнение станет выглядеть так:
(2 sin x + cos
x)( sin x + cos
x) = 0.
Произведение двух выражений равно нулю.
Значит, либо первое выражение равно нулю, либо – второе, либо оба вместе.
«Либо» означает совокупность двух уравнений, а не систему.
Запишем совокупность.
Решаем уравнения по порядку.
Решаем первое уравнение:
Помечтаем.
Можно выразить cos x через sin x.
Возникнет квадратный корень.
Придется возводить в квадрат.
Получится квадратное уравнение относительно sin x.
Попробуем по-другому.
Есть формула:
a sin x + b cos x = 
sin(x
+ α)
, где α = arctg
В выражении
a = 2,
b = 1,
значит, по приведенной формуле:
=
sin(x
+ α)
, где α = arctg
.
Уравнение
превратилось
в такое:
sin(x + α) = 0.
На
можно
поделить обе части уравнения.
Справа
по-прежнему будет ноль.
Получим:
sin(x + α) = 0.
Решение
этого уравнения:
x + α = πk
, где k
Z.
Выразим икс:
x = - α + πk
, где k Z,
α = arctg .
Окончательно решение уравнения
выглядит так:
x = - arctg + πk
, где k Z.
Но к «альфе» еще придется вернуться.
Решаем второе уравнение совокупности.
Снова применим
формулу
a sin x + b cos x = sin(x + α)
, где α = arctg
.
На этот раз
для выражения:
a = 1,
b = ,
значит, по
этой формуле
, где α = arctg
.
Значит,
уравнение
станет
таким:
.
На
можно
поделить обе части уравнения.
Если
посчитать,
=2.
Но можно и
не считать – все равно делить.
Справа
по-прежнему будет ноль.
Уравнение
станет
таким:
, где α = arctg
.
Если
поделить на 1, получим:
α = arctg .
А, если
вспомнить табличное значение:
= .
Значит:
arctg = 
.
Уравнение
решаем так же, как предыдущее, только
«альфа» имеет другое значение.
x + α = πk
, где k Z,
Выразим икс:
x = - α + πk
, где k Z,
α = .
Окончательно решение уравнения
выглядит так:
x = - + πk
, где k Z.
Объединим
полученные решения в совокупность:
.
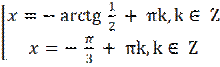Это - ответ
на первое задание (решить уравнение).
Займемся
вторым вопросом.
Найти корни уравнения
2 + sin x cos x + (sin
2x +
) =
0,
принадлежащие промежутку
[; ].
Вспомним, что корни уравнения определяются по формулам:
и
.
Корней бесконечно много, но нас просят
отобрать только корни, принадлежащие промежутку
[; ]..
Фактически, требуется определить, для каких значений параметра «k», корни попадут в промежуток [; ].
Конечно, надо корни изобразить точками на окружности.
(Единичная окружность или нет, в данном случае неважно. Главное, что она
– круглая. И эта ее «круглость» правильно показывает периодичность
тригонометрических функций.)
Где на окружности точка, соответствующая углу
Сравним этот
угол с углами, тангенсы которых имеют табличные значения.
Поскольку
речь идет об арктангенсе, заодно вспомним значения тангенса соответствующих
углов.
tg 0 = 0
tg 
= 
tg 
= 1
tg =
Угол альфа,
который нас интересует, имеет тангенс, равный одной второй:
Тангенс – функция возрастающая.
И, т.к. значение
< 1
и
,
альфа лежит
в пределах от 0 до .
Как, насчет 
Сравним
∨
Возведем каждое из
сравниваемых чисел в квадрат, получим:
∨
Т.к.
<,
следовательно:
<.
Следовательно:
<.
Можно
рисовать окружность.
Она
изображена на рисунке 1.
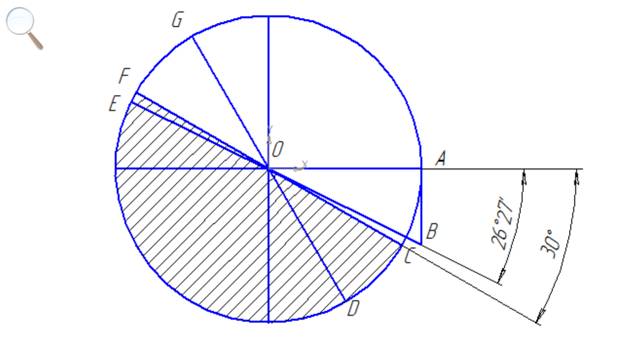
Рисунок 1 Окружность.
Что на
рисунке.
Окружность.
Что за
точки:
Точка О –
центр окружности.
Точка А соответствует
нулевому углу, а также углам 
.
Точка B соответствует углу AOB. Величина этого угла является корнем
уравнения:
2 sin x + cos x = 0,
и принимает
значения:
Кстати, в △AOB OA = 2 AB. Для наглядности, отрезок AB специально проведен
перпендикулярно отрезку OA, чтобы △AOB был прямоугольным. Длина отрезка AB выбрана в два раза меньшей
длины отрезка OA для того, чтобы
tg ∠ AOB = 
.
Следовательно
∠ AOB = .
Здесь угол
отсчитываем по часовой стрелке.
Точка C соответствует
углу 
Точка D соответствует
углу AOD. Величина этого угла является корнем уравнения:
sin x + cos x = 0,
и принимает
значения:
.
Точка E соответствует
углу AOE. Величина этого угла является корнем уравнения:
2 sin x + cos x = 0,
и принимает
значения:
Точка F соответствует
углу 
Точка G соответствует
углу AOG. Величина этого угла является корнем уравнения:
sin x + cos x = 0,
и принимает
значения:
.
Для того чтобы
наглядно показать как незначительно отличаются величины 
, на рисунке 1 указаны величины углов
AOB и AJC, отсчитанные по часовой стрелке.
Заштрихованная
область соответствует промежутку [; ].
Из рисунка
видно, что условию задания 2 удовлетворяют углы, соответствующие точкам E и D.
Корни
исходного уравнения, принадлежащие промежутку [; ]:
и 
.