Учебные материалы Шарапова М.П.
12-я задача диагностики
Второй способ решения
© Шарапов Михаил Петрович, 2021-12-02
Первый способ решения см. здесь…
Решение
Требуется,
чтобы делилось на 24.
И сумма цифр
чтобы была 24.
Здесь везде
имеется в виду, конечно, деление без остатка.
Число
Обозначим
искомое число
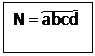
Черта
означает, что abcd не
перемножаются, а просто являются цифрами числа.
Найдем их –
найдем число.
Найдем число
– решим задачу.
Учет
делимости на 24
Т.к.
24 = 3 x 8
Чтобы число
делилось на 24, надо, чтобы оно делилось на 3 и на 8.
Специально
проверять делимость на 3 не надо, т.к. по признаку делимости на 3, число
делится на 3, если сумма цифр его делится на 3.
По условию
сумма цифр 24, делится на 3, следовательно, и все число делится на 3.
Проверять
делимость на 8 тяжело, но мы будем проверять делимость на 4.
Ведь, если
число должно делиться на 8, то оно должно делиться и на 4.
Обратное
неверно.
A
По условию
1500 < N < 2000
Следовательно
a = 1
Соотношения
a + b + c + d = 24
Поскольку a, b, c, d – цифры (десятичные, хотя – в условии
об этом ни гу-гу).
0 ![]() a
a ![]()
0 ![]() b
b ![]()
0 ![]() c
c ![]()
0 ![]() d
d ![]()
a = 1
Значит
1 + b + c + d = 24
b + c + d = 23
d = 23 - b – c
Упростит
перебор учет делимости N на 4.
Ведь, если N должно делиться на 24, оно должно
делиться и на 4.
Для
делимости на 4 надо, чтобы число, составленное из 2-х последних цифр в неизменном
порядке, делилось на 4.
![]() cd
cd
делилось на 4.
Цифра d
Т.к.
d = 23 - b - C
даже, если
b = 9
и
c = 9
d = 23 - 9 – 9 = 14 – 9 = 5
А, если b и c меньше 9, или хотя бы одно из них
меньше 9, d должно
быть больше.
Кроме того, d должно быть четным.
Ведь, если
число должно делиться на 4, то уж на 2 оно тоже должно делиться.
По признаку
делимости на 2 четное число должно оканчиваться четной цифрой.
Т.е.
d = 6
или
d = 8
Если
d = 6
На сумму
b + c
останется
b + c = 23 – d = 23 – 6 = 17
Либо
b = 9
c = 8
Либо
b = 8
c = 9
Число из
двух последних цифр, которое должно делиться на 4, будет
Либо
86
либо
96
На 4 делится
только
96.
Следовательно,
N = 1896
Не забываем
проверить делимость на 8.
Делится
1896 = 8 x 237
Если
d = 8
На сумму
b + c
останется
b + c = 23 – d = 23 – 8 = 15
Либо
b = 9
c = 6
Число из
двух последних цифр, которое должно делиться на 4, будет
68
68 делится
на 4.
N = 1968
Не забываем
проверить делимость на 8.
Делится
1968 = 8 x 246
Либо
b = 8
c = 7
Число из
двух последних цифр, которое должно делиться на 4, будет
78
Не делится 4
Либо
b = 7
c = 8
Число из
двух последних цифр, которое должно делиться на 4, будет
88
Делится на
4.
N = 1788
Не забываем
проверить делимость на 8.
Не делится
Либо
b = 6
c = 9
Число из
двух последних цифр, которое должно делиться на 4, будет
98
Не делится.
Итак
N = 1968
Либо
N = 1896
Уф-ф!